演算法系列#9 Two heaps

在很多問題中，題目給了我們一堆的 element，我們可以將他們分成兩個部分，並且針對兩個部分其中一個尋找最小值，另一個尋找最大值。

這個方法我們會使用兩個 heap

例如我們在尋找中位數時就可以用這個方法，講 elements 分成兩個部分並且分別放入 Min heap 跟 Max heap，中位數就能從這兩個 heap 的頂部得到了

這邊要特別講 heap 的結構以及時間複雜度

heap

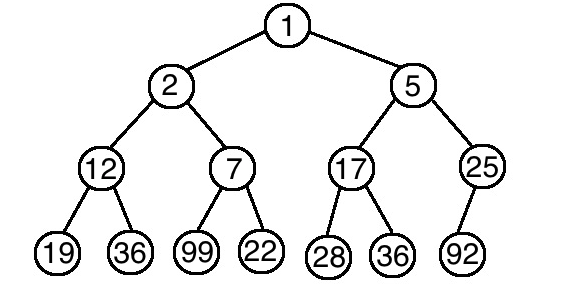
heap 是一個 binary tree 的結構，並且保持平衡

heap 的平衡指的是如果你是 min heap 那麼父節點的大小都比子節點還要小，max heap 則相反

如下圖就是一個 min heap

要插入一個元素到 heap 裡面，通常會是直接插進最底部的 leaf node，並且依序跟他的父節點做比較，直到符合平衡，因此 worst case 會是從 leaf node 一路比較到 root，時間複雜度是 O(logn)

通常刪除的會是 heap 最頂端也就是最小或是最大的數字，刪掉後會直接從 leaf node 的最後一個拿上來遞補 root 的位置，再接著往下做比較，時間複雜度也是從 root 一路比到 leaf node 是 O(logn)

那麼如果要從一堆 elements 開始建立一個 heap 的話就是將這 n 個 elements 插入到 heap 所以是 O(nlogn) 嗎？

其實不是，詳細的算法有點複雜這裡就不做討論，能告訴給你的結論是，建立 heap 的時間複雜度是 O(n)，如果想知道怎麼來的話可以參考這裡